01. Clustering Coefficient
Clustering Coefficient
Measuring the degree to which nodes in a network tend to "cluster" or form triangles.
Triadic Closure
The tendency for people who share connections in a social network to become connected.
Local Clustering Coefficient
Fraction of pairs of the node's friends that are friends with each other.
Compute the local clustering coefficient of node C:
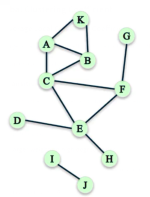
# of pairs of C's friends =
Assume that the local clustering coefficient of a node of degree less than 2 to be 0.
nx.clustering(G, 'F')Global Clustering Coefficient
1) Average Local Clustering Coefficient
Average local clustering coefficient over all nodes in the graph.
nx.average_clustering(G)2) Transitivity
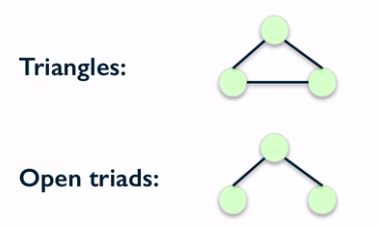
Ratio of number of triangles and number of "open triads".
Triangles
Open triads
Puts larger weight on high degree nodes
nx.transitivity(G)Transitivity vs Average Clustering Coefficient
- Both measure the tendency for edges to form triangles.
- Transitivity weights nodes with large degree higher.
02. Distance Measures
Distance
Path
A sequence of nodes connected by an edge.
Distance between two nodes
The length of the shortest path between them.
nx.shortest_path(G, 'A', 'H')
nx.shortest_path_length(G, 'A', 'H')Finding the distance from node A to every other node
Breadth-First Search
T = nx.bfs_tree(G, 'A')
T.edges()
nx.shortest_path_length(G, 'A')Distance Measures
Characterizing distance in a graph
Average distance
Average distance between every pair of nodes.
nx.average_shortest_path_length(G)Diameter
Maximum distance between any pair of nodes.
nx.diameter(G)Eccentricity
The eccentricity of a node n is the largest distance from n to all other nodes.
nx.eccentricity(G)Radius
The minimum eccentricity in the graph.
nx.radius(G)Identifying central and peripheral nodes
Periphery
The set of nodes with eccentricity = diameter
nx.periphery(G)Center
The set of nodes with eccentricity = radius
nx.center(G)Example: Karate Club Network
G = nx.karate_club_graph()
G = nx.convert_node_labels_to_integers(G, first_label=1)03. Connected Components
Connectivity in Undirected Graph
Connected Graph
For every pair nodes, there is a path between them.
nx.is_connected(G)Connected Components
A subset of nodes such as:
- Every node in the subset has a path to every other node.
- No other node has a path to any node in the subset.
nx.number_connected_components(G)
sorted(nx.connected_components(G))
nx.node_connected_componenet(G, 'M')Connectivity in Directed Graph
Strongly connected
For every pair nodes u and v, there is a directed path from u to v and a directed path from v to u.
nx.is_strongly_connected(G)Weakly connected
A directed graph is weakly connected if replacing all directed edges with undirected edges produces a connected undirected graph.
nx.is_weakly_connected(G)Strongly connected components
A subset of nodes such as:
- Every node in the subset has a directed path to every other node.
- No other node has a directed path to and from every node in the subset.
sorted(x.strongly_connected_components(G))Weakly connected components
The connected components of the graph after replacing all directed edges with undirected edges.
sorted(nx.weakly_connected_components(G))04. Network Robustness
Connectivity and Robustness in Network
Network Robustness
The ability of a network to maintain its general structural properties when it faces failure or attacks.
Type of attacks: removal of nodes or edges.
Structural properties connectivity.
Disconnecting a Graph
What is the smallest number of nodes that can be removed from this graph in order to disconnect it.
nx.node_connectivity(G_un)Which nodes?
nx.minimum_node_cut(G_un)What is the smallest number of edges that can be removed from this graph in order to disconnect it.
nx.edge_connectivity(G_un)Which edges?
nx.minimum_edge_cut(G_un)Robust networks have large minimum node and edge cuts.
Simple Paths
Options for messages from G to L
sorted(nx.all_simple_paths(G, 'G', 'L'))Node Connectivity
If we wanted to block the message from G to L by removing nodes from the network, how many nodes would we need to remove?
nx.node_connectivity(G_un, 'G', 'L')Which nodes?
nx.minimum_node_cut(G_un, 'G', 'L')Edge Connectivity
If we wanted to block the message from G to L by removing edges from the network, how many nodes would we need to remove?
nx.edge_connectivity(G_un, 'G', 'L')Which edges ?
nx.minimum_edge_cut(G_un, 'G', 'L')Graphs with large node and edge connectivity are more robust to the loss of nodes and edges.